discretize.base.BaseMesh

class discretize.base.BaseMesh(n, x0=None, **kwargs)

Bases: properties.base.base.HasProperties, discretize.mixins.vtkModule.vtkInterface

BaseMesh does all the counting you don’t want to do. BaseMesh should be inherited by meshes with a regular structure.

Required Properties:

• axis_u (Vector3): Vector orientation of u-direction. For more details see the docs for the rotation_matrix property., a 3D Vector of <class ‘float’> with shape (3), Default: X
• axis_v (Vector3): Vector orientation of v-direction. For more details see the docs for the rotation_matrix property., a 3D Vector of <class ‘float’> with shape (3), Default: Y
• axis_w (Vector3): Vector orientation of w-direction. For more details see the docs for the rotation_matrix property., a 3D Vector of <class ‘float’> with shape (3), Default: Z
• reference_system (String): The type of coordinate reference frame. Can take on the values cartesian, cylindrical, or spherical. Abbreviations of these are allowed., a unicode string, Default: cartesian
• x0 (Array): origin of the mesh (dim, ), a list or numpy array of <class ‘float’> with shape (*)

Attributes

BaseMesh.axis_u

X

Type:axis_u (Vector3) Type:Vector orientation of u-direction. For more details see the docs for the rotation_matrix property., a 3D Vector of <class ‘float’> with shape (3), Default

BaseMesh.axis_v

Y

Type:axis_v (Vector3) Type:Vector orientation of v-direction. For more details see the docs for the rotation_matrix property., a 3D Vector of <class ‘float’> with shape (3), Default

BaseMesh.axis_w

Z

Type:axis_w (Vector3) Type:Vector orientation of w-direction. For more details see the docs for the rotation_matrix property., a 3D Vector of <class ‘float’> with shape (3), Default

BaseMesh.dim

The dimension of the mesh (1, 2, or 3).

Returns:dimension of the mesh Return type:int

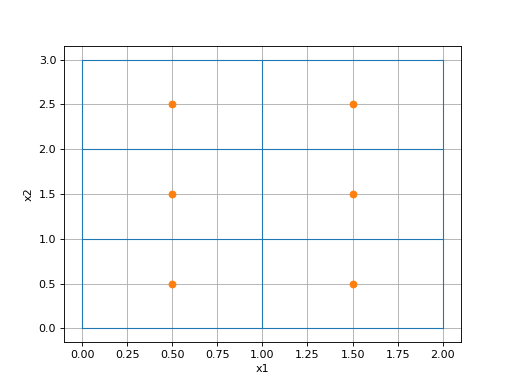
BaseMesh.nC

Total number of cells in the mesh.

Returns:number of cells in the mesh Return type:int

Example

import discretize
import numpy as np
mesh = discretize.TensorMesh([np.ones(n) for n in [2,3]])
mesh.plotGrid(centers=True, showIt=True)

print(mesh.nC)

(Source code, png, hires.png, pdf)

BaseMesh.nE

Total number of edges.

Returns:nE Return type:int = sum([nEx, nEy, nEz])

BaseMesh.nEx

Number of x-edges

Returns:nEx Return type:int

BaseMesh.nEy

Number of y-edges

Returns:nEy Return type:int

BaseMesh.nEz

Number of z-edges

Returns:nEz Return type:int

BaseMesh.nF

Total number of faces.

Return type:int Returns:sum([nFx, nFy, nFz])

BaseMesh.nFx

Number of x-faces

Return type:int Returns:nFx

BaseMesh.nFy

Number of y-faces

Return type:int Returns:nFy

BaseMesh.nFz

Number of z-faces

Return type:int Returns:nFz

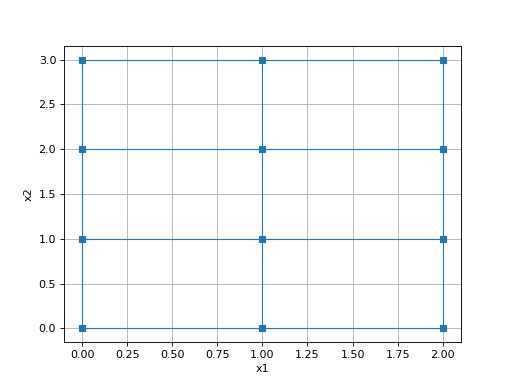
BaseMesh.nN

Total number of nodes

Returns:number of nodes in the mesh Return type:int

Example

import discretize
import numpy as np
mesh = discretize.TensorMesh([np.ones(n) for n in [2,3]])
mesh.plotGrid(nodes=True, showIt=True)

print(mesh.nN)

(Source code, png, hires.png, pdf)

BaseMesh.normals

Face Normals

Return type:numpy.ndarray Returns:normals, (sum(nF), dim)

BaseMesh.reference_is_rotated

True if the axes are rotated from the traditional <X,Y,Z> system with vectors of \((1,0,0)\), \((0,1,0)\), and \((0,0,1)\)

BaseMesh.reference_system

cartesian

Type:reference_system (String) Type:The type of coordinate reference frame. Can take on the values cartesian, cylindrical, or spherical. Abbreviations of these are allowed., a unicode string, Default

BaseMesh.rotation_matrix

Builds a rotation matrix to transform coordinates from their coordinate system into a conventional cartesian system. This is built off of the three axis_u, axis_v, and axis_w properties; these mapping coordinates use the letters U, V, and W (the three letters preceding X, Y, and Z in the alphabet) to define the projection of the X, Y, and Z durections. These UVW vectors describe the placement and transformation of the mesh’s coordinate sytem assuming at most 3 directions.

Why would you want to use these UVW mapping vectors the this rotation_matrix property? They allow us to define the realationship between local and global coordinate systems and provide a tool for switching between the two while still maintaing the connectivity of the mesh’s cells. For a visual example of this, please see the figure in the docs for the vtkInterface.

BaseMesh.tangents

Edge Tangents

Return type:numpy.ndarray Returns:normals, (sum(nE), dim)

BaseMesh.vnE

Total number of edges in each direction

Returns:

• vnE (numpy.ndarray = [nEx, nEy, nEz], (dim, ))
• .. plot:: – :include-source:

  import discretize import numpy as np M = discretize.TensorMesh([np.ones(n) for n in [2,3]]) M.plotGrid(edges=True, showIt=True)

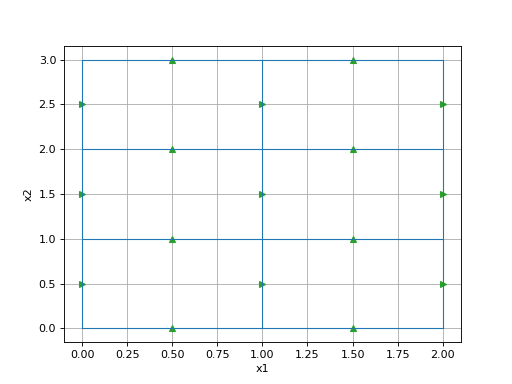
BaseMesh.vnF

Total number of faces in each direction

Return type:numpy.ndarray Returns:[nFx, nFy, nFz], (dim, )

import discretize
import numpy as np
M = discretize.TensorMesh([np.ones(n) for n in [2,3]])
M.plotGrid(faces=True, showIt=True)

(Source code, png, hires.png, pdf)

BaseMesh.x0

origin of the mesh (dim, ), a list or numpy array of <class ‘float’> with shape (*)

Type:x0 (Array)

Methods

BaseMesh.copy()

Make a copy of the current mesh

classmethod BaseMesh.deserialize(value, trusted=False, strict=False, assert_valid=False, **kwargs)

Creates HasProperties instance from serialized dictionary

This uses the Property deserializers to deserialize all JSON-compatible dictionary values into their corresponding Property values on a new instance of a HasProperties class. Extra keys in the dictionary that do not correspond to Properties will be ignored.

Parameters:

• value - Dictionary to deserialize new instance from.
• trusted - If True (and if the input dictionary has '__class__' keyword and this class is in the registry), the new HasProperties class will come from the dictionary. If False (the default), only the HasProperties class this method is called on will be constructed.
• strict - Requires '__class__', if present on the input dictionary, to match the deserialized instance’s class. Also disallows unused properties in the input dictionary. Default is False.
• assert_valid - Require deserialized instance to be valid. Default is False.
• Any other keyword arguments will be passed through to the Property deserializers.

BaseMesh.equal(other)

Determine if two HasProperties instances are equivalent

Equivalence is determined by checking if all Property values on two instances are equal, using Property.equal.

BaseMesh.projectEdgeVector(eV)

Given a vector, eV, in cartesian coordinates, this will project it onto the mesh using the tangents

Parameters:eV (numpy.ndarray) – edge vector with shape (nE, dim) Return type:numpy.ndarray Returns:projected edge vector, (nE, )

BaseMesh.projectFaceVector(fV)

Given a vector, fV, in cartesian coordinates, this will project it onto the mesh using the normals

Parameters:fV (numpy.ndarray) – face vector with shape (nF, dim) Return type:numpy.ndarray Returns:projected face vector, (nF, )

BaseMesh.save(filename='mesh.json', verbose=False)

Save the mesh to json :param str file: filename for saving the casing properties :param str directory: working directory for saving the file

BaseMesh.serialize(include_class=True, save_dynamic=False, **kwargs)

Serializes a HasProperties instance to dictionary

This uses the Property serializers to serialize all Property values to a JSON-compatible dictionary. Properties that are undefined are not included. If the HasProperties instance contains a reference to itself, a properties.SelfReferenceError will be raised.

Parameters:

• include_class - If True (the default), the name of the class will also be saved to the serialized dictionary under key '__class__'
• save_dynamic - If True, dynamic properties are written to the serialized dict (default: False).
• Any other keyword arguments will be passed through to the Property serializers.

BaseMesh.toVTK(models=None)

Convert this mesh object to it’s proper vtki data object with the given model dictionary as the cell data of that dataset.

Parameters:models (dict(numpy.ndarray)) – Name(‘s) and array(‘s). Match number of cells

BaseMesh.validate()

Call all registered class validator methods

These are all methods decorated with @properties.validator. Validator methods are expected to raise a ValidationError if they fail.

BaseMesh.writeVTK(fileName, models=None, directory='')

Makes and saves a VTK object from this mesh and given models

Parameters:

• fileName (str) – path to the output vtk file or just its name if directory is specified
• models (dict) – dictionary of numpy.array - Name(‘s) and array(‘s). Match number of cells
• directory (str) – directory where the UBC GIF file lives