Basic Forward 2D DC Resistivity

2D DC forward modeling example with Tensor and Curvilinear Meshes

import discretize
from pymatsolver import SolverLU
import numpy as np
import matplotlib.pyplot as plt


def run(plotIt=True):


    # Step1: Generate Tensor and Curvilinear Mesh
    sz = [40, 40]
    tM = discretize.TensorMesh(sz)
    rM = discretize.CurvilinearMesh(discretize.utils.exampleLrmGrid(sz, 'rotate'))

    # Step2: Direct Current (DC) operator
    def DCfun(mesh, pts):
        D = mesh.faceDiv
        sigma = 1e-2*np.ones(mesh.nC)
        MsigI = mesh.getFaceInnerProduct(sigma, invProp=True, invMat=True)
        A = -D*MsigI*D.T
        A[-1, -1] /= mesh.vol[-1]  # Remove null space
        rhs = np.zeros(mesh.nC)
        txind = discretize.utils.closestPoints(mesh, pts)
        rhs[txind] = np.r_[1, -1]
        return A, rhs

    pts = np.vstack((np.r_[0.25, 0.5], np.r_[0.75, 0.5]))

    # Step3: Solve DC problem (LU solver)
    AtM, rhstM = DCfun(tM, pts)
    AinvtM = SolverLU(AtM)
    phitM = AinvtM*rhstM

    ArM, rhsrM = DCfun(rM, pts)
    AinvrM = SolverLU(ArM)
    phirM = AinvrM*rhsrM

    if not plotIt:
        return

    # Step4: Making Figure
    fig, axes = plt.subplots(1, 2, figsize=(12*1.2, 4*1.2))
    vmin, vmax = phitM.min(), phitM.max()
    dat = tM.plotImage(phitM, ax=axes[0], clim=(vmin, vmax), grid=True)
    dat = rM.plotImage(phirM, ax=axes[1], clim=(vmin, vmax), grid=True)
    cb0 = plt.colorbar(dat[0], ax=axes[0])
    cb1 = plt.colorbar(dat[0], ax=axes[1])
    cb0.set_label("Voltage (V)")
    cb1.set_label("Voltage (V)")

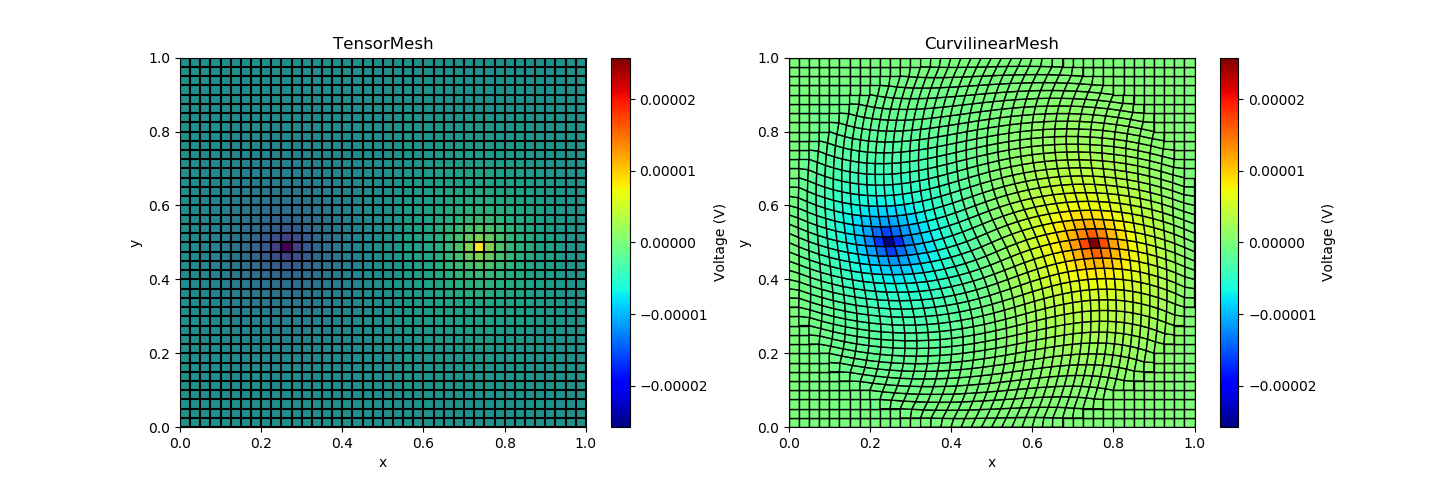
    axes[0].set_title('TensorMesh')
    axes[1].set_title('CurvilinearMesh')


if __name__ == '__main__':
    run()
    plt.show()

Total running time of the script: ( 0 minutes 1.567 seconds)