discretize.TensorMesh

class discretize.TensorMesh(h=None, x0=None, **kwargs)

Bases: discretize.base.base_tensor_mesh.BaseTensorMesh, discretize.base.base_mesh.BaseRectangularMesh, discretize.View.TensorView, discretize.DiffOperators.DiffOperators, discretize.InnerProducts.InnerProducts, discretize.MeshIO.TensorMeshIO

TensorMesh is a mesh class that deals with tensor product meshes.

Any Mesh that has a constant width along the entire axis such that it can defined by a single width vector, called ‘h’.

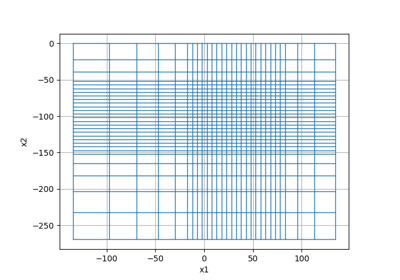
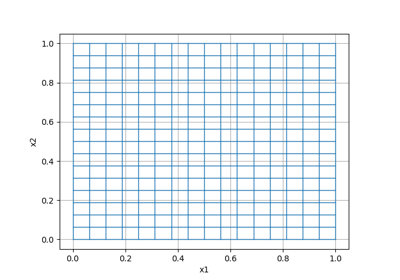
import discretize

hx = np.array([1, 1, 1])
hy = np.array([1, 2])
hz = np.array([1, 1, 1, 1])

mesh = discretize.TensorMesh([hx, hy, hz])
mesh.plotGrid()

(Source code)

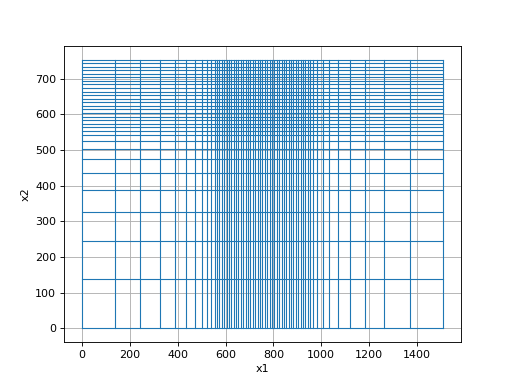
Example of a padded tensor mesh using discretize.utils.meshTensor():

import discretize
mesh = discretize.TensorMesh([
    [(10, 10, -1.3), (10, 40), (10, 10, 1.3)],
    [(10, 10, -1.3), (10, 20)]
])
mesh.plotGrid()

(Source code)

For a quick tensor mesh on a (10x12x15) unit cube

import discretize
mesh = discretize.TensorMesh([10, 12, 15])

Required Properties:

• axis_u (Vector3): Vector orientation of u-direction. For more details see the docs for the rotation_matrix property., a 3D Vector of <class ‘float’> with shape (3), Default: X
• axis_v (Vector3): Vector orientation of v-direction. For more details see the docs for the rotation_matrix property., a 3D Vector of <class ‘float’> with shape (3), Default: Y
• axis_w (Vector3): Vector orientation of w-direction. For more details see the docs for the rotation_matrix property., a 3D Vector of <class ‘float’> with shape (3), Default: Z
• h (a list of Array): h is a list containing the cell widths of the tensor mesh in each dimension., a list (each item is a list or numpy array of <class ‘float’> with shape (*)) with length between 0 and 3
• reference_system (String): The type of coordinate reference frame. Can take on the values cartesian, cylindrical, or spherical. Abbreviations of these are allowed., a unicode string, Default: cartesian
• x0 (Array): origin of the mesh (dim, ), a list or numpy array of <class ‘float’> with shape (*)

Examples using discretize.TensorMesh

Tensor: Creation

Mesh Types

Plotting: Streamline thickness

Basic: PlotImage

Basic Forward 2D DC Resistivity

Operators: Cahn Hilliard

Tensor meshes

Overview of mesh types

Attributes

TensorMesh.area

Construct face areas of the 3D model as 1d array.

TensorMesh.areaFx

Area of the x-faces

TensorMesh.areaFy

Area of the y-faces

TensorMesh.areaFz

Area of the z-faces

TensorMesh.aveCC2F

Construct the averaging operator on cell centers to faces.

TensorMesh.aveCCV2F

Construct the averaging operator on cell centers to faces as a vector.

TensorMesh.aveE2CC

Construct the averaging operator on cell edges to cell centers.

TensorMesh.aveE2CCV

Construct the averaging operator on cell edges to cell centers.

TensorMesh.aveEx2CC

Construct the averaging operator on cell edges in the x direction to cell centers.

TensorMesh.aveEy2CC

Construct the averaging operator on cell edges in the y direction to cell centers.

TensorMesh.aveEz2CC

Construct the averaging operator on cell edges in the z direction to cell centers.

TensorMesh.aveF2CC

Construct the averaging operator on cell faces to cell centers.

TensorMesh.aveF2CCV

Construct the averaging operator on cell faces to cell centers.

TensorMesh.aveFx2CC

Construct the averaging operator on cell faces in the x direction to cell centers.

TensorMesh.aveFy2CC

Construct the averaging operator on cell faces in the y direction to cell centers.

TensorMesh.aveFz2CC

Construct the averaging operator on cell faces in the z direction to cell centers.

TensorMesh.aveN2CC

Construct the averaging operator on cell nodes to cell centers.

TensorMesh.aveN2E

Construct the averaging operator on cell nodes to cell edges, keeping each dimension separate.

TensorMesh.aveN2F

Construct the averaging operator on cell nodes to cell faces, keeping each dimension separate.

TensorMesh.axis_u

X

Type:axis_u (Vector3) Type:Vector orientation of u-direction. For more details see the docs for the rotation_matrix property., a 3D Vector of <class ‘float’> with shape (3), Default

TensorMesh.axis_v

Y

Type:axis_v (Vector3) Type:Vector orientation of v-direction. For more details see the docs for the rotation_matrix property., a 3D Vector of <class ‘float’> with shape (3), Default

TensorMesh.axis_w

Z

Type:axis_w (Vector3) Type:Vector orientation of w-direction. For more details see the docs for the rotation_matrix property., a 3D Vector of <class ‘float’> with shape (3), Default

TensorMesh.cellBoundaryInd

Find indices of boundary faces in each direction

TensorMesh.cellGrad

The cell centered Gradient, takes you to cell faces.

TensorMesh.cellGradBC

The cell centered Gradient boundary condition matrix

TensorMesh.cellGradx

Cell centered Gradient in the x dimension. Has neumann boundary conditions.

TensorMesh.cellGrady

TensorMesh.cellGradz

Cell centered Gradient in the x dimension. Has neumann boundary conditions.

TensorMesh.dim

The dimension of the mesh (1, 2, or 3).

Returns:dimension of the mesh Return type:int

TensorMesh.edge

Construct edge legnths of the 3D model as 1d array.

TensorMesh.edgeCurl

Construct the 3D curl operator.

TensorMesh.edgeEx

x-edge lengths

TensorMesh.edgeEy

y-edge lengths

TensorMesh.edgeEz

z-edge lengths

TensorMesh.faceBoundaryInd

Find indices of boundary faces in each direction

TensorMesh.faceDiv

Construct divergence operator (face-stg to cell-centres).

TensorMesh.faceDivx

Construct divergence operator in the x component (face-stg to cell-centres).

TensorMesh.faceDivy

TensorMesh.faceDivz

Construct divergence operator in the z component (face-stg to cell-centers).

TensorMesh.gridCC

Cell-centered grid.

TensorMesh.gridEx

Edge staggered grid in the x direction.

TensorMesh.gridEy

Edge staggered grid in the y direction.

TensorMesh.gridEz

Edge staggered grid in the z direction.

TensorMesh.gridFx

Face staggered grid in the x direction.

TensorMesh.gridFy

Face staggered grid in the y direction.

TensorMesh.gridFz

Face staggered grid in the z direction.

TensorMesh.gridN

Nodal grid.

TensorMesh.h

h is a list containing the cell widths of the tensor mesh in each dimension., a list (each item is a list or numpy array of <class ‘float’> with shape (*)) with length between 0 and 3

Type:h (a list of Array)

TensorMesh.h_gridded

Returns an (nC, dim) numpy array with the widths of all cells in order

TensorMesh.hx

Width of cells in the x direction

TensorMesh.hy

Width of cells in the y direction

TensorMesh.hz

Width of cells in the z direction

TensorMesh.nC

Total number of cells

Return type:int Returns:nC

TensorMesh.nCx

Number of cells in the x direction

Return type:int Returns:nCx

TensorMesh.nCy

Number of cells in the y direction

Return type:int Returns:nCy or None if dim < 2

TensorMesh.nCz

Number of cells in the z direction

Return type:int Returns:nCz or None if dim < 3

TensorMesh.nE

Total number of edges.

Returns:nE Return type:int = sum([nEx, nEy, nEz])

TensorMesh.nEx

Number of x-edges

Return type:int Returns:nEx

TensorMesh.nEy

Number of y-edges

Return type:int Returns:nEy

TensorMesh.nEz

Number of z-edges

Return type:int Returns:nEz

TensorMesh.nF

Total number of faces.

Return type:int Returns:sum([nFx, nFy, nFz])

TensorMesh.nFx

Number of x-faces

Return type:int Returns:nFx

TensorMesh.nFy

Number of y-faces

Return type:int Returns:nFy

TensorMesh.nFz

Number of z-faces

Return type:int Returns:nFz

TensorMesh.nN

Total number of nodes

Return type:int Returns:nN

TensorMesh.nNx

Number of nodes in the x-direction

Return type:int Returns:nNx

TensorMesh.nNy

Number of nodes in the y-direction

Return type:int Returns:nNy or None if dim < 2

TensorMesh.nNz

Number of nodes in the z-direction

Return type:int Returns:nNz or None if dim < 3

TensorMesh.nodalGrad

Construct gradient operator (nodes to edges).

TensorMesh.nodalLaplacian

Construct laplacian operator (nodes to edges).

TensorMesh.normals

Face Normals

Return type:numpy.ndarray Returns:normals, (sum(nF), dim)

TensorMesh.reference_is_rotated

True if the axes are rotated from the traditional <X,Y,Z> system with vectors of \((1,0,0)\), \((0,1,0)\), and \((0,0,1)\)

TensorMesh.reference_system

cartesian

Type:reference_system (String) Type:The type of coordinate reference frame. Can take on the values cartesian, cylindrical, or spherical. Abbreviations of these are allowed., a unicode string, Default

TensorMesh.rotation_matrix

Builds a rotation matrix to transform coordinates from their coordinate system into a conventional cartesian system. This is built off of the three axis_u, axis_v, and axis_w properties; these mapping coordinates use the letters U, V, and W (the three letters preceding X, Y, and Z in the alphabet) to define the projection of the X, Y, and Z durections. These UVW vectors describe the placement and transformation of the mesh’s coordinate sytem assuming at most 3 directions.

Why would you want to use these UVW mapping vectors the this rotation_matrix property? They allow us to define the realationship between local and global coordinate systems and provide a tool for switching between the two while still maintaing the connectivity of the mesh’s cells. For a visual example of this, please see the figure in the docs for the vtkInterface.

TensorMesh.tangents

Edge Tangents

Return type:numpy.ndarray Returns:normals, (sum(nE), dim)

TensorMesh.vectorCCx

Cell-centered grid vector (1D) in the x direction.

TensorMesh.vectorCCy

Cell-centered grid vector (1D) in the y direction.

TensorMesh.vectorCCz

Cell-centered grid vector (1D) in the z direction.

TensorMesh.vectorNx

Nodal grid vector (1D) in the x direction.

TensorMesh.vectorNy

Nodal grid vector (1D) in the y direction.

TensorMesh.vectorNz

Nodal grid vector (1D) in the z direction.

TensorMesh.vnC

Total number of cells in each direction

Return type:numpy.ndarray Returns:[nCx, nCy, nCz]

TensorMesh.vnE

Total number of edges in each direction

Returns:

• vnE (numpy.ndarray = [nEx, nEy, nEz], (dim, ))
• .. plot:: – :include-source:

  import discretize import numpy as np M = discretize.TensorMesh([np.ones(n) for n in [2,3]]) M.plotGrid(edges=True, showIt=True)

TensorMesh.vnEx

Number of x-edges in each direction

Return type:numpy.ndarray Returns:vnEx

TensorMesh.vnEy

Number of y-edges in each direction

Return type:numpy.ndarray Returns:vnEy or None if dim < 2

TensorMesh.vnEz

Number of z-edges in each direction

Return type:numpy.ndarray Returns:vnEz or None if dim < 3

TensorMesh.vnF

Total number of faces in each direction

Return type:numpy.ndarray Returns:[nFx, nFy, nFz], (dim, )

import discretize
import numpy as np
M = discretize.TensorMesh([np.ones(n) for n in [2,3]])
M.plotGrid(faces=True, showIt=True)

(Source code)

TensorMesh.vnFx

Number of x-faces in each direction

Return type:numpy.ndarray Returns:vnFx

TensorMesh.vnFy

Number of y-faces in each direction

Return type:numpy.ndarray Returns:vnFy or None if dim < 2

TensorMesh.vnFz

Number of z-faces in each direction

Return type:numpy.ndarray Returns:vnFz or None if dim < 3

TensorMesh.vnN

Total number of nodes in each direction

Return type:numpy.ndarray Returns:[nNx, nNy, nNz]

TensorMesh.vol

Construct cell volumes of the 3D model as 1d array.

TensorMesh.x0

origin of the mesh (dim, ), a list or numpy array of <class ‘float’> with shape (*)

Type:x0 (Array)

Methods

TensorMesh.copy()

Make a copy of the current mesh

classmethod TensorMesh.deserialize(value, trusted=False, strict=False, assert_valid=False, **kwargs)

Creates HasProperties instance from serialized dictionary

This uses the Property deserializers to deserialize all JSON-compatible dictionary values into their corresponding Property values on a new instance of a HasProperties class. Extra keys in the dictionary that do not correspond to Properties will be ignored.

Parameters:

• value - Dictionary to deserialize new instance from.
• trusted - If True (and if the input dictionary has '__class__' keyword and this class is in the registry), the new HasProperties class will come from the dictionary. If False (the default), only the HasProperties class this method is called on will be constructed.
• strict - Requires '__class__', if present on the input dictionary, to match the deserialized instance’s class. Also disallows unused properties in the input dictionary. Default is False.
• assert_valid - Require deserialized instance to be valid. Default is False.
• Any other keyword arguments will be passed through to the Property deserializers.

TensorMesh.equal(other)

Determine if two HasProperties instances are equivalent

Equivalence is determined by checking if all Property values on two instances are equal, using Property.equal.

TensorMesh.getBCProjWF(BC, discretization='CC')

The weak form boundary condition projection matrices.

Example

# Neumann in all directions
BC = 'neumann'

# 3D, Dirichlet in y Neumann else
BC = ['neumann', 'dirichlet', 'neumann']

# 3D, Neumann in x on bottom of domain, Dirichlet else
BC = [['neumann', 'dirichlet'], 'dirichlet', 'dirichlet']

TensorMesh.getBCProjWF_simple(discretization='CC')

The weak form boundary condition projection matrices when mixed boundary condition is used

TensorMesh.getEdgeInnerProduct(prop=None, invProp=False, invMat=False, doFast=True)

Generate the edge inner product matrix

Parameters:

• prop (numpy.ndarray) – material property (tensor properties are possible) at each cell center (nC, (1, 3, or 6))
• invProp (bool) – inverts the material property
• invMat (bool) – inverts the matrix
• doFast (bool) – do a faster implementation if available.

Returns:

M, the inner product matrix (nE, nE)

Return type:

scipy.sparse.csr_matrix

TensorMesh.getEdgeInnerProductDeriv(prop, doFast=True, invProp=False, invMat=False)

Parameters:

• prop (numpy.ndarray) – material property (tensor properties are possible) at each cell center (nC, (1, 3, or 6))
• doFast (bool) – do a faster implementation if available.
• invProp (bool) – inverts the material property
• invMat (bool) – inverts the matrix

Returns:

dMdm, the derivative of the inner product matrix (nE, nC*nA)

Return type:

scipy.sparse.csr_matrix

TensorMesh.getFaceInnerProduct(prop=None, invProp=False, invMat=False, doFast=True)

Generate the face inner product matrix

Parameters:

• prop (numpy.ndarray) – material property (tensor properties are possible) at each cell center (nC, (1, 3, or 6))
• invProp (bool) – inverts the material property
• invMat (bool) – inverts the matrix
• doFast (bool) – do a faster implementation if available.

Returns:

M, the inner product matrix (nF, nF)

Return type:

scipy.sparse.csr_matrix

TensorMesh.getFaceInnerProductDeriv(prop, doFast=True, invProp=False, invMat=False)

Parameters:

• prop (numpy.ndarray) – material property (tensor properties are possible) at each cell center (nC, (1, 3, or 6))
• doFast – bool do a faster implementation if available.
• invProp (bool) – inverts the material property
• invMat (bool) – inverts the matrix

Returns:

dMdmu(u), the derivative of the inner product matrix for a certain u

Return type:

scipy.sparse.csr_matrix

TensorMesh.getInterpolationMat(loc, locType='CC', zerosOutside=False)

Produces interpolation matrix

Parameters:

• loc (numpy.ndarray) – Location of points to interpolate to
• locType (str) –

  What to interpolate (see below)

  locType can be:

  'Ex'    -> x-component of field defined on edges
  'Ey'    -> y-component of field defined on edges
  'Ez'    -> z-component of field defined on edges
  'Fx'    -> x-component of field defined on faces
  'Fy'    -> y-component of field defined on faces
  'Fz'    -> z-component of field defined on faces
  'N'     -> scalar field defined on nodes
  'CC'    -> scalar field defined on cell centers
  'CCVx'  -> x-component of vector field defined on cell centers
  'CCVy'  -> y-component of vector field defined on cell centers
  'CCVz'  -> z-component of vector field defined on cell centers
  

Returns:

M, the interpolation matrix

Return type:

scipy.sparse.csr_matrix

TensorMesh.getTensor(key)

Returns a tensor list.

Parameters:key (str) –

Which tensor (see below)

key can be:

'CC'    -> scalar field defined on cell centers
'N'     -> scalar field defined on nodes
'Fx'    -> x-component of field defined on faces
'Fy'    -> y-component of field defined on faces
'Fz'    -> z-component of field defined on faces
'Ex'    -> x-component of field defined on edges
'Ey'    -> y-component of field defined on edges
'Ez'    -> z-component of field defined on edges

Returns:list of the tensors that make up the mesh. Return type:list

TensorMesh.isInside(pts, locType='N')

Determines if a set of points are inside a mesh.

Parameters:pts (numpy.ndarray) – Location of points to test Return type:numpy.ndarray Returns:inside, numpy array of booleans

TensorMesh.plotGrid(ax=None, nodes=False, faces=False, centers=False, edges=False, lines=True, showIt=False, **kwargs)

Plot the nodal, cell-centered and staggered grids for 1,2 and 3 dimensions.

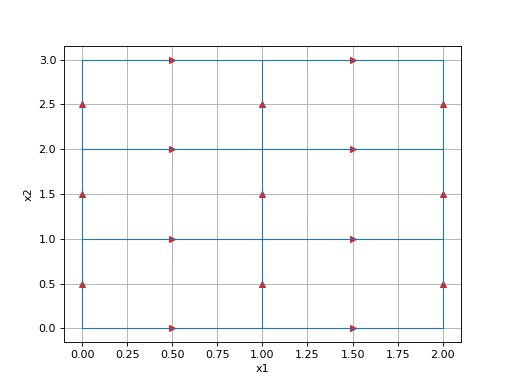
Parameters:

• nodes (bool) – plot nodes
• faces (bool) – plot faces
• centers (bool) – plot centers
• edges (bool) – plot edges
• lines (bool) – plot lines connecting nodes
• showIt (bool) – call plt.show()

import discretize
import numpy as np
h1 = np.linspace(.1, .5, 3)
h2 = np.linspace(.1, .5, 5)
mesh = discretize.TensorMesh([h1, h2])
mesh.plotGrid(nodes=True, faces=True, centers=True, lines=True, showIt=True)

(Source code)

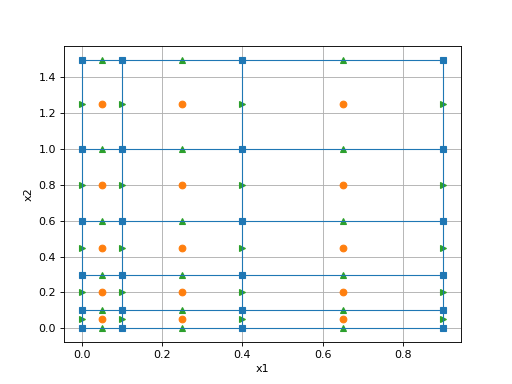
import discretize
import numpy as np
h1 = np.linspace(.1, .5, 3)
h2 = np.linspace(.1, .5, 5)
h3 = np.linspace(.1, .5, 3)
mesh = discretize.TensorMesh([h1, h2, h3])
mesh.plotGrid(nodes=True, faces=True, centers=True, lines=True, showIt=True)

(Source code)

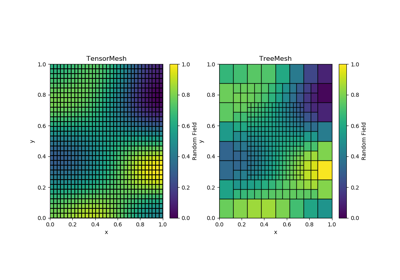
TensorMesh.plotImage(v)

Plots scalar fields on the given mesh.

Input:

Parameters:v (numpy.ndarray) – vector

Optional Inputs:

Parameters:

• vType (str) – type of vector (‘CC’, ‘N’, ‘F’, ‘Fx’, ‘Fy’, ‘Fz’, ‘E’, ‘Ex’, ‘Ey’, ‘Ez’)
• ax (matplotlib.axes.Axes) – axis to plot to
• showIt (bool) – call plt.show()

3D Inputs:

Parameters:

• numbering (bool) – show numbering of slices, 3D only
• annotationColor (str) – color of annotation, e.g. ‘w’, ‘k’, ‘b’

import discretize
import numpy as np
M = discretize.TensorMesh([20, 20])
v = np.sin(M.gridCC[:, 0]*2*np.pi)*np.sin(M.gridCC[:, 1]*2*np.pi)
M.plotImage(v, showIt=True)

(Source code)

import discretize
import numpy as np
M = discretize.TensorMesh([20, 20, 20])
v = np.sin(M.gridCC[:, 0]*2*np.pi)*np.sin(M.gridCC[:, 1]*2*np.pi)*np.sin(M.gridCC[:, 2]*2*np.pi)
M.plotImage(v, annotationColor='k', showIt=True)

(Source code)

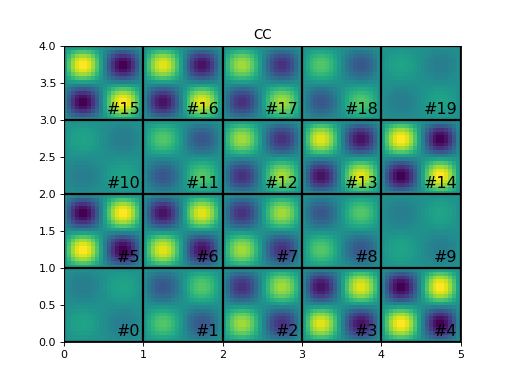
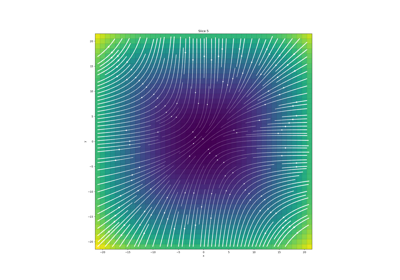
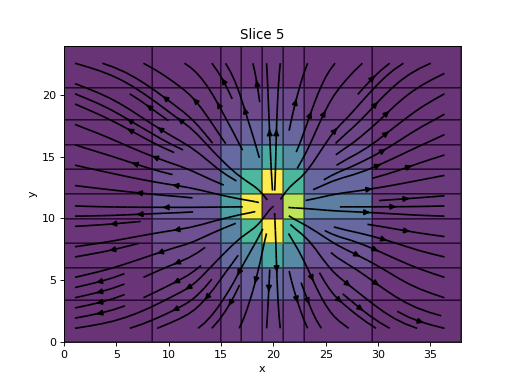
TensorMesh.plotSlice(v, vType='CC', normal='Z', ind=None, grid=False, view='real', ax=None, clim=None, showIt=False, pcolorOpts=None, streamOpts=None, gridOpts=None, range_x=None, range_y=None, sample_grid=None, stream_threshold=None, stream_thickness=None)

Plots a slice of a 3D mesh.

(Source code)

TensorMesh.plot_3d_slicer(v, xslice=None, yslice=None, zslice=None, vType='CC', view='real', axis='xy', transparent=None, clim=None, aspect='auto', grid=[2, 2, 1], pcolorOpts=None)

Plot slices of a 3D volume, interactively (scroll wheel).

If called from a notebook, make sure to set

%matplotlib notebook

See the class discretize.View.Slicer for more information.

It returns nothing. However, if you need the different figure handles you can get it via

fig = plt.gcf()

and subsequently its children via

fig.get_children()

and recursively deeper, e.g.,

fig.get_children()[0].get_children().

TensorMesh.projectEdgeVector(eV)

Given a vector, eV, in cartesian coordinates, this will project it onto the mesh using the tangents

Parameters:eV (numpy.ndarray) – edge vector with shape (nE, dim) Return type:numpy.ndarray Returns:projected edge vector, (nE, )

TensorMesh.projectFaceVector(fV)

Given a vector, fV, in cartesian coordinates, this will project it onto the mesh using the normals

Parameters:fV (numpy.ndarray) – face vector with shape (nF, dim) Return type:numpy.ndarray Returns:projected face vector, (nF, )

TensorMesh.r(x, xType='CC', outType='CC', format='V')

r is a quick reshape command that will do the best it can at giving you what you want.

For example, you have a face variable, and you want the x component of it reshaped to a 3D matrix.

r can fulfil your dreams:

mesh.r(V, 'F', 'Fx', 'M')
       |   |     |    |
       |   |     |    {
       |   |     |      How: 'M' or ['V'] for a matrix
       |   |     |      (ndgrid style) or a vector (n x dim)
       |   |     |    }
       |   |     {
       |   |       What you want: ['CC'], 'N',
       |   |                       'F', 'Fx', 'Fy', 'Fz',
       |   |                       'E', 'Ex', 'Ey', or 'Ez'
       |   |     }
       |   {
       |     What is it: ['CC'], 'N',
       |                  'F', 'Fx', 'Fy', 'Fz',
       |                  'E', 'Ex', 'Ey', or 'Ez'
       |   }
       {
         The input: as a list or ndarray
       }

For example:

# Separates each component of the Ex grid into 3 matrices
Xex, Yex, Zex = r(mesh.gridEx, 'Ex', 'Ex', 'M')

# Given an edge vector, return just the x edges as a vector
XedgeVector = r(edgeVector, 'E', 'Ex', 'V')

# Separates each component of the edgeVector into 3 vectors
eX, eY, eZ = r(edgeVector, 'E', 'E', 'V')

TensorMesh.readModelUBC(fileName, directory='')

Read UBC 2D or 3D Tensor mesh model

and generate Tensor mesh model

Input: :param str fileName: path to the UBC GIF mesh file to read or just its name if directory is specified :param str directory: directory where the UBC GIF file lives

Output: :rtype: numpy.ndarray :return: model with TensorMesh ordered

classmethod TensorMesh.readUBC(fileName, directory='')

Wrapper to Read UBC GIF 2D and 3D tensor mesh and generate same dimension TensorMesh.

Input: :param str fileName: path to the UBC GIF mesh file or just its name if directory is specified :param str directory: directory where the UBC GIF file lives

Output: :rtype: TensorMesh :return: The tensor mesh for the fileName.

classmethod TensorMesh.readVTK(fileName, directory='')

Read VTK Rectilinear (vtr xml file) and return Tensor mesh and model

Parameters:

• fileName (str) – path to the vtr model file to read or just its name if directory is specified
• directory (str) – directory where the UBC GIF file lives

Returns:

(TensorMesh, modelDictionary)

Return type:

tuple

TensorMesh.save(filename='mesh.json', verbose=False)

Save the mesh to json :param str file: filename for saving the casing properties :param str directory: working directory for saving the file

TensorMesh.serialize(include_class=True, save_dynamic=False, **kwargs)

Serializes a HasProperties instance to dictionary

This uses the Property serializers to serialize all Property values to a JSON-compatible dictionary. Properties that are undefined are not included. If the HasProperties instance contains a reference to itself, a properties.SelfReferenceError will be raised.

Parameters:

• include_class - If True (the default), the name of the class will also be saved to the serialized dictionary under key '__class__'
• save_dynamic - If True, dynamic properties are written to the serialized dict (default: False).
• Any other keyword arguments will be passed through to the Property serializers.

TensorMesh.setCellGradBC(BC)

Function that sets the boundary conditions for cell-centred derivative operators.

Example

..code:: python

# Neumann in all directions BC = ‘neumann’

# 3D, Dirichlet in y Neumann else BC = [‘neumann’, ‘dirichlet’, ‘neumann’]

# 3D, Neumann in x on bottom of domain, Dirichlet else BC = [[‘neumann’, ‘dirichlet’], ‘dirichlet’, ‘dirichlet’]

TensorMesh.toVTK(models=None)

Convert this mesh object to it’s proper vtki data object with the given model dictionary as the cell data of that dataset.

Parameters:models (dict(numpy.ndarray)) – Name(‘s) and array(‘s). Match number of cells

TensorMesh.validate()

Call all registered class validator methods

These are all methods decorated with @properties.validator. Validator methods are expected to raise a ValidationError if they fail.

TensorMesh.writeModelUBC(fileName, model, directory='')

Writes a model associated with a TensorMesh to a UBC-GIF format model file.

Input: :param str fileName: File to write to or just its name if directory is specified :param str directory: directory where the UBC GIF file lives :param numpy.ndarray model: The model

TensorMesh.writeUBC(fileName, models=None, directory='', comment_lines='')

Writes a TensorMesh to a UBC-GIF format mesh file.

Input: :param str fileName: File to write to :param str directory: directory where to save model :param dict models: A dictionary of the models :param str comment_lines: comment lines preceded with ‘!’ to add

TensorMesh.writeVTK(fileName, models=None, directory='')

Makes and saves a VTK object from this mesh and given models

Parameters:

• fileName (str) – path to the output vtk file or just its name if directory is specified
• models (dict) – dictionary of numpy.array - Name(‘s) and array(‘s). Match number of cells
• directory (str) – directory where the UBC GIF file lives